Strongly Connected Components

Strongly Connected Components (SCCs) are a fundamental concept in graph theory and algorithms. In a directed graph, a Strongly Connected Component is a subset of vertices where every vertex in the subset is reachable from every other vertex in the same subset by traversing the directed edges. Finding the SCCs of a graph can provide important insights into the structure and connectivity of the graph, with applications in various fields such as social network analysis, web crawling, and network routing . This tutorial will explore the definition, properties, and efficient algorithms for identifying Strongly Connected Components in graph data structures

Table of Content

• What is Strongly Connected Components (SCCs)?
• Why Strongly Connected Components (SCCs) are Important?
• Difference Between Connected and Strongly Connected Components (SCCs)
• Why conventional DFS method cannot be used to find strongly connected components?
• Connecting Two Strongly Connected Component by a Unidirectional Edge
• Brute Force Approach for Finding Strongly Connected Components
• Efficient Approach for Finding Strongly Connected Components (SCCs)
  • 1. Kosaraju’s Algorithm:
  • 2. Tarjan’s Algorithm:

  What is Strongly Connected Components (SCCs)?

  A strongly connected component of a directed graph is a maximal subgraph where every pair of vertices is mutually reachable. This means that for any two nodes A and B in this subgraph, there is a path from A to B and a path from B to A.

  For example: The below graph has two strongly connected components and since there is path from each vertex to every other vertex in the same strongly connected component.

  

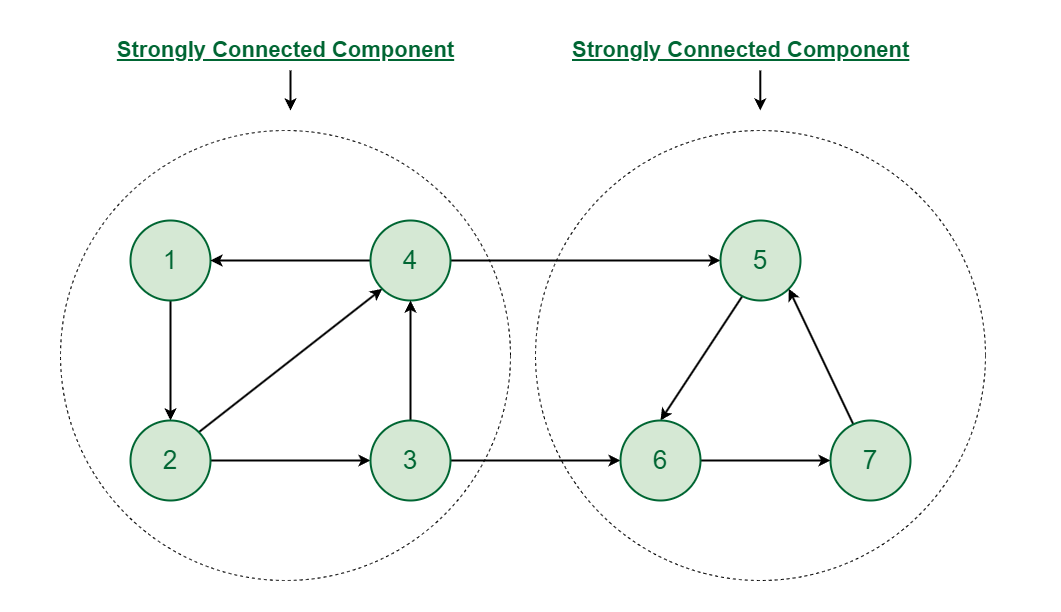
  Strongly Connected Component

  Why Strongly Connected Components (SCCs) are Important?

  Understanding SCCs is crucial for various applications such as:

  • Network Analysis : Identifying clusters of tightly interconnected nodes.
  • Optimizing Web Crawlers : Determining parts of the web graph that are closely linked.
  • Dependency Resolution : In software, understanding which modules are interdependent.

  Difference Between Connected and Strongly Connected Components ( SCCs)

  Connectivity in a undirected graph refers to whether two vertices are reachable from each other or not. Two vertices are said to be connected if there is path between them. Meanwhile Strongly Connected is applicable only to directed graphs . A subgraph of a directed graph is considered to be an Strongly Connected Components (SCC) if and only if for every pair of vertices A and B , there exists a path from A to B and a path from B to A . Let’s see why the standard dfs method to find connnected components in a graph cannot be used to determine strongly connected components.

  

  

  Now, let’s start a dfs call from vertex 1 to visit other vertices.

  Why conventional DFS method cannot be used to find the strongly connected components?

  All the vertices can be reached from vertex 1. But vertices 1 and 5,6,7 can not be in the same strongly connected component because there is no directed path from vertex 5,6 or 7 to vertex 1. The graph has two strongly connected components and . So the conventional dfs method cannot be used to find the strongly connected components.

  Connecting Two Strongly Connected Component by a Unidirectional Edge

  Two different connected components becomes a single component if a edge is added between a vertex from one component to a vertex of other component. But this is not the case in strongly connected components. Two strongly connected components doesn’t become a single strongly connected component if there is only a unidirectional edge from one SCC to other SCC.

  

  Brute Force Approach for Finding Strongly Connected Components

  The simple method will be for each vertex i (which is not a part of any strongly component) find the vertices which will be the part of strongly connected component containing vertex i. Two vertex i and j will be in the same strongly connected component if they there is a directed path from vertex i to vertex j and vice-versa.

  

  Let’s understand the approach with the help of following example:

  • Starting with vertex 1. There is path from vertex 1 to vertex 2 and vice-versa. Similarly there is a path from vertex 1 to vertex 3 and vice versa. So, vertex 2 and 3 will be in the same Strongly Connected Component as vertex 1. Although there is directed path form vertex 1 to vertex 4 and vertex 5. But there is no directed path from vertex 4,5 to vertex 1 so vertex 4 and 5 won’t be in the same Strongly Connected Component as vertex 1. Thus Vertex 1,2 and 3 forms a Strongly Connected Component.
  • For Vertex 2 and 3, there Strongly Connected Component has already been determined.
  • For Vertex 4, there is a path from vertex 4 to vertex 5 but there is no path from vertex 5 to vertex 4. So vertex 4 and 5 won’t be in the Same Strongly Connected Component. So both Vertex 4 and Vertex 5 will be part of Single Strongly Connected Component.
  • Hence there will be 3 Strongly Connected Component , and .

  Below is the implementation of above approach:

                                                                                                                                 of any SCC                   there is a path from vertex i to  current SCC list.                                                                                       Java